| Uploader: | Goldenhammer |
| Date Added: | 17.02.2019 |
| File Size: | 73.84 Mb |
| Operating Systems: | Windows NT/2000/XP/2003/2003/7/8/10 MacOS 10/X |
| Downloads: | 22456 |
| Price: | Free* [*Free Regsitration Required] |
Standard scores and normal distributions | Nurse Key
17 Standard scores and normal distributions Chapter Contents Introduction Standard scores (z scores) Normal distributions The standard normal curve Calculations of areas under the normal curve Critical values Standard normal curves for the comparison of distributions Summary Introduction In this chapter we will discuss standard distributions. Chapter 5: Normal Probability Distributions - Solutions Note: All areas and z-scores are approximate. Your answers may vary slightly. Normal Distributions: Finding Probabilities If you are given that a random variable X has a normal distribution, finding probabilities corresponds to finding the area between the standard normal curve and the x-axis, using the table of z-scores. Standard deviation to one. Example: The average grade on a quiz was 41 points with a standard deviation of 3. Label both bell curves. Normal distribution. Std. distribution. This is really just finding the z-scores!! 32 35 38 41 44 47 -2 -1 0 1 2 3.
Free download of standard normal distribution of z-scores
Standard normal curves for the comparison of distributions. In this chapter we will discuss standard distributions. Standard scores represent the position of a score or measurement in relation to an overall set of scores. Standard distributions are also useful for comparing scores from different sets of measurements. Standard free download of standard normal distribution of z-scores are used in both clinical practice and research in the health sciences.
In clinical practice the score of a patient is often compared with a known distribution to interpret the score. Describe the characteristics of normal and standard normal curves. Show how standard normal curves can be used for calculating percentile ranks. Show how standard normal curves can be used to compare scores from different distributions. Consider this example: infant A walked unaided at the age of 40 weeks, while infant B is 65 weeks old but still cannot walk.
What sense can we make of these measurements? Could infant B need further clinical investigation in case he has some neurological abnormality? The fact that infant B is unable to walk at the age of 65 weeks is not very informative in the absence of additional information about how this compares with norms for other children.
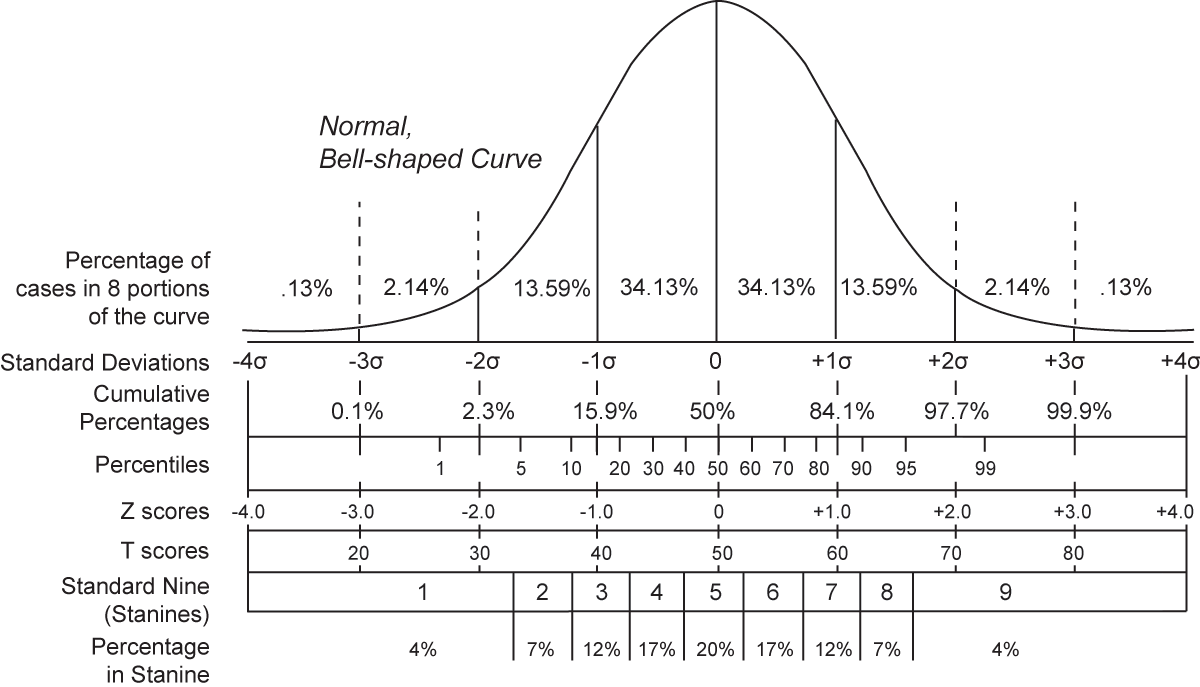
Assuming that the frequency distribution is normal, the frequency polygon representing the population would look something like that free download of standard normal distribution of z-scores in Figure Figure The process of transforming a score into a measurement based on its distance from the mean in standard deviations is called standardizing the score.
A z score represents how many standard deviations a given raw score is above or below the mean. The equation for transforming specific raw scores into z scores is given as:. For the above equation, x is the raw score, or µ is the mean of the distribution from which the score was drawn and s or σ is the standard deviation of the distribution. That is, when we know the mean and standard deviation of a distribution, we can transform any raw score into a z score.
Conversely, when the z score is known, we can use the above equations to calculate the corresponding raw scores. In other words, A walked very early and B was a very late starter. The particular value of standardizing scores for understanding clinical or research evidence will be discussed in the context of the concepts of normal and standard normal distributions. What is meant by a normal distribution is illustrated by the normal curve see Fig, free download of standard normal distribution of z-scores.
We assume here that the variable x has been measured on an interval or ratio scale and that it is a continuous variable such as weight, height or blood pressure. Relatively few cases fall into the high or low values of x. Most of the cases fall close to the mean. For the theoretical normal distribution, the arms of the curve do not intersect with the x-axis, allowing for a few extreme scores.
The precise equation for the normal curve was discovered by the mathematician Gauss, so that it is sometimes referred to as a Gaussian curve. We need not worry about the actual formula for the normal curve. Rather, the point is that, given that the functional relationship between f and x is known, integral calculus can be used to calculate areas under the curve for any value of x.
All normal curves have the same general mathematical form; whether we are graphing IQ or weight, the same bell shape will appear. The only differences between the curves are the mean value and the amount of variation. This is why the mean and the standard deviation provide us with important information about any particular normal distribution.
Note that it is unlikely that any real data are exactly normally distributed. Rather, the normal distribution is a mathematical model that is useful for representing real distributions. If we transform the raw scores of a variable into z scores and then plot the frequency polygon for the distribution, we will have a standard curve. If the original distribution was normal, then the frequency polygon will be a standard normal curve. Standard normal curves are identical regardless of the nature of the original variables, free download of standard normal distribution of z-scores.
By transforming raw scores into z scores we are adjusting for differences in means and standard deviations, which are the only things that distinguish between non-standardized normal curves, free download of standard normal distribution of z-scores.
The mean is always 0 zero. The standard deviation of z scores is always 1 one. For instance, the z score for 55 which is one standard deviation above the mean is:.
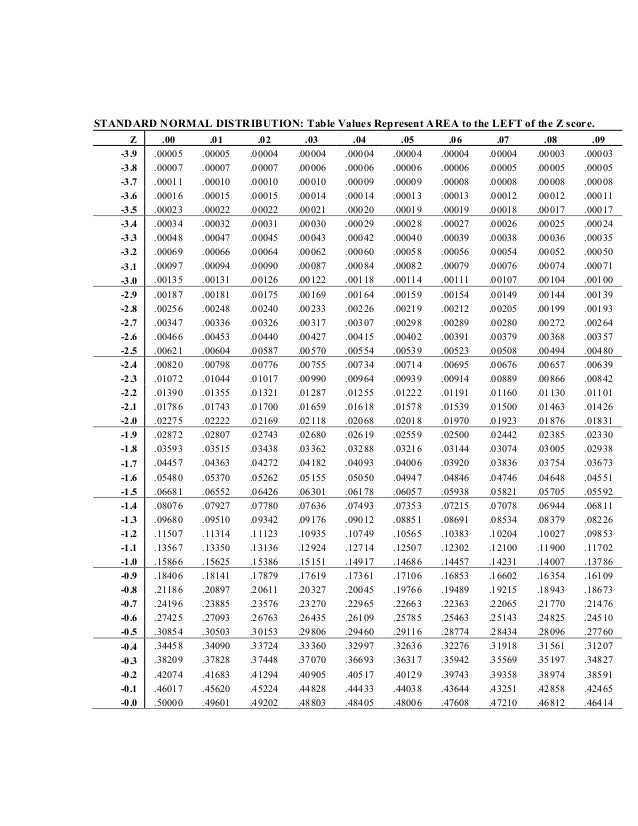
It is assumed that the total area under the curve adds up to 1. Since the normal curve is symmetrical, 0. More generally, we can use appropriate statistical tables to estimate the area under the standard normal curve for any given z scores. These areas are available in table form see Appendix A so that for any value of z we can read off the corresponding area. The area under the curve between any two points is free download of standard normal distribution of z-scores proportional to the percentage of cases falling above, below or between those two points.
We can use the standard normal curve to calculate the percentage of scores falling between any specified two scores. Standard scores and normal distributions. Introduction In this chapter we will discuss standard distributions. The aims of this chapter are to: 1. Standard scores z scores Consider this example: infant A walked unaided at the age of 40 weeks, while infant B is 65 weeks old but still cannot walk.
The standard normal curve If we transform the raw scores of a variable into z scores and then plot the frequency polygon for the distribution, we will have a standard curve. The standard normal curve has the following additional properties: 1. For instance, the z score for 55 which is one standard deviation above the mean is: 4. Only gold members can continue reading.
Log In or Register to continue. You may also need Measures of central tendency and variability Correlation Measurement Observation Interviewing techniques The research process Surveys and quasi-experimental designs Effect size and the interpretation of evidence. Tags: Introduction to Research in the Health Sciences.
Normal Distribution \u0026 Z-scores
, time: 10:20Free download of standard normal distribution of z-scores
The standard normal distribution table gives the probability of a regularly distributed random variable Z, whose mean is equivalent to 0 and difference equal to 1, is not exactly or equal to z. The normal distribution is a persistent probability distribution. It is also called Gaussian distribution. It is pertinent for positive estimations of z only. When you are trying to find the area between two negative z scores, you will need to perform a few more calculations. The truth is that you will be trying to discover the area or proportion of the standard normal distribution to the left of the lowest z score value as well as the area or proportion of the standard normal distribution to the right of the highest z score value. As soon as you. Standard deviation to one. Example: The average grade on a quiz was 41 points with a standard deviation of 3. Label both bell curves. Normal distribution. Std. distribution. This is really just finding the z-scores!! 32 35 38 41 44 47 -2 -1 0 1 2 3.

No comments:
Post a Comment